--- title: The Kissing Problem in Three Dimensions tags: optimization, kissing-number-problem --- # The Kissing Problem in Three Dimensions 報告者：105201518 林育愷 107201002 李家妤 Reference ~ * Musin, Oleg. (2006). [*The Kissing Problem in Three Dimensions*](https://arxiv.org/pdf/math/0410324.pdf). Discrete & Computational Geometry. 35. 375-384. 10.1007/s00454-005-1201-3. * Musin, O. (2008). [*The Kissing Number in Four Dimensions*](https://arxiv.org/pdf/math/0309430.pdf). Annals of Mathematics, 168(1), second series, 1-32. * Pfender, Florian & Ziegler, Günter. (2004). [*Kissing Numbers, Sphere Packings, and Some Unexpected Proofs*](http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=D008876F67DF9FFF08805E12C80C743A?doi=10.1.1.408.1138&rep=rep1&type=pdf). Notices of the American Mathematical Society.  Abstract ~ 此篇論文在探討在三維空間中最多有多少單位球可以不重疊貼合在一單位球上，其中使用到微積分的觀念以及一些基本的球面幾何。 ## 歷史進展 ### 克卜勒猜想與親吻數問題 在三維空間中布置一顆單位球──在部分文章中為了方便介紹會給他一個顏色──我們不妨稱之為紅球，我們想要找到最多有多少顆同樣大小的藍球，可以同時與位於中心的紅球「親吻」，也就是觸碰的意思，這是在三維空間上的親吻數問題 (kissing number problem)。 親吻數問題的探悉可以幫助理解最密堆疊問題 (sphere packing problem)，這個議題是說：找出在 $n$ 維度歐式空間中使密度最高的堆疊方法。而克卜勒猜想 (Kepler conjecture) 則是根據自然現象的觀察，猜想在三維空間下面心力方 (FCC) 與六方最密堆疊 (HCP) 是堆疊問題的最佳解，而他們的堆疊密度落在 $\pi/\sqrt{18}\approx 0.74$. 至少在二維空間來說，光是六方最密堆疊就產生出平面上晶格堆疊最佳解問題、平面上最密堆疊問題、以及二維的親吻數問題，而這些問題在拉高到空間甚至之上的維度時，整體就會變得相當複雜了。 | <img src="https://hackmd.mcl.math.ncu.edu.tw/uploads/upload_bfcb56320a10df232393edd42ed511b3.png" width=400> | <img src="https://hackmd.mcl.math.ncu.edu.tw/uploads/upload_22f16c117715198f942debabb8656e87.png" width=400> | | ------------------------------------------------------------------------------------------------------------ | ------------------------------------------------------------------------------------------------------------ | | 面心立方 (黑色圓點代表球心) | 六方最密堆疊 | > 面心立方來源：https://en.wikipedia.org/wiki/Cubic_crystal_system > 六方最密堆疊來源：http://lampx.tugraz.at/~hadley/ss1/crystalstructure/structures/hcp/hcp.php 回到我們的主題，在一維數線上，親吻數這個問題是顯而易見的：左右各一顆球，總共二顆；在平面上也沒有太多煩惱：以球為中心依照角度劃分六等分，在每個等分射線上擺上一顆球，總共六顆完美地包覆中心球。 但遺憾地，在三維空間上就是一道難題了──即使至今站在巨人肩膀上的我們已有了解答，仍需要一些筆墨去妥善設計其數學模型，並且對這項問題給出完備的解釋。 答案是十二顆，考慮空間上球心的佈點，他會正好成一個正二十面體。不過在十七世紀末還沒有結論的時代中，大衛‧葛瑞高里 (David Gregory) 可不這麼認為。 |  | 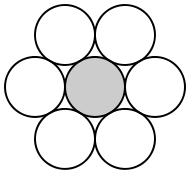 | 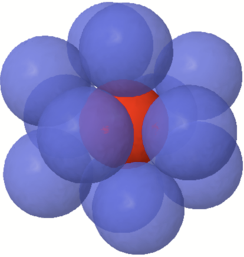 | | ------------------------------------------------------------------------------------------- | ------------------------------------------------------------------------------------------- | ------------------------------------------------------------------------------------------- | | 一維親吻數 | 二維親吻數 | 三維親吻數 | > source: wiki ### 牛頓與葛瑞高里 舉出十二顆的例子這件事情並不是問題困難的地方，當然很多原因在於這個例子在幾何上也具備一定的特殊性──最困難的地方在於你需要給出足夠的證據表明「不存在十三顆的擺設方法」。說明其不存在的方式，不外乎得使用反證法，給予條件後並在推論中找出其中矛盾之處。 當時雖然沒有人能完成這項工作，但人們總不免對這件事情有一些猜測。其中最為著名的兩派說法便是牛頓與葛瑞高里，牛頓認為三維親吻數就是十二；而葛瑞高里認為應該是十三。 而兩位科學家最終也沒有取得共識，其正解亦沉潛了近兩個世紀後，方有個水落石出。 | <img src="https://codimd.mcl.math.ncu.edu.tw/uploads/upload_a773c469e41fcb1505305dfc87077e78.png" width=200 > | <img src="https://codimd.mcl.math.ncu.edu.tw/uploads/upload_82e54c8fba3901f9ff18a8542ccc1076.png" width=200 > | | ------------------------------------------------------------------------------------------------------------- | ------------------------------------------------------------------------------------------------------------- | | 牛頓 | 葛瑞高里 | > source: wiki ### 二十世紀中 在二十世紀中期，有許多數學家對此議題提出解法，首先是 Reinhold Hoppe 在 1894 年時提出一個解法，但所使用的方法有些錯誤，黑爾斯 (Thomas Hales)~[2]~ 在之後也發表文章分析 Reinhold Hoppe 方法的問題；最後許特 (Kurt Schütte) 與 範德瓦爾登 (van der Waerden) 在 1953 年給出了第一分完整的證明~[3]~，隨後 1956 年里希 (John Leech) 提出了一個優雅證明的草圖~[4]~，其後 Aigner 和 Ziegler 也將里希提出的證明完成~[5]~；在近代，也有許多數學家提出更多更簡潔的方法來解決這個問題，而本篇文章深入探討的方法也是其中之一 ── Oleg R. Musin 在 2006 年所發表的文章~[6]~。 | <img src="https://codimd.mcl.math.ncu.edu.tw/uploads/upload_01dd4d4339e17876185def67540b94fb.png" width=200 > | <img src="https://codimd.mcl.math.ncu.edu.tw/uploads/upload_a4cbf8e93eb4e05960f3e2f68c900171.png" width=180 > | <img src="https://codimd.mcl.math.ncu.edu.tw/uploads/upload_6c9eb64e415128a11bc23a53b5728c3b.png" width=150 > | <img src="https://codimd.mcl.math.ncu.edu.tw/uploads/upload_5c22f84c678d4d00f2153493343a2222.png" width=180 > | | ------------------------------------------------------------------------------------------------------------- | ------------------------------------------------------------------------------------------------------------- | ------------------------------------------------------------------------------------------------------------- | ------------------------------------------------------------------------------------------------------------- | | Musin | Kurt Schütte | van der Waerden | John Leech | ### 其餘維度 除了三維空間的親吻數之外，數學家也想了解在其他維度空間中的親吻數分別為多少，紛紛展開了研究，但不幸的是目前大於三維的維度空間中僅有四維、八維與二十四維空間有著精確的解答，其餘維度目前都僅能估計出其上下界。目前在 24 維度以下的親吻數上下界如下表： | Dimension | Lower bound | Upper bound | |:---------:|:-----------:|:-----------:| | 1 | 2 | | | 2 | 6 | | | 3 | 12 | | | 4 | 24 | | | 5 | 40 | 44 | | 6 | 72 | 78 | | 7 | 126 | 134 | | 8 | 240 | | | 9 | 306 | 364 | | 10 | 500 | 554 | | 11 | 582 | 870 | | 12 | 840 | 1,357 | | 13 | 1,154 | 2,069 | | 14 | 1,606 | 3,183 | | 15 | 2,564 | 4,866 | | 16 | 4,320 | 7,355 | | 17 | 5,346 | 11,072 | | 18 | 7,398 | 16,572 | | 19 | 10,668 | 24,812 | | 20 | 17,400 | 36,764 | | 21 | 27,720 | 54,584 | | 22 | 49,896 | 82,340 | | 23 | 93,150 | 124,416 | | 24 | 196,560 | |  ## 結合球面幾何性質與最佳化工具的證明手法 事實上三維親吻數問題在 1953 年就有第一份完整的證明，Kurt Schütte 與 Bartel Leendert van der Waerden 的研究工作，去說明 12 這件事情。而我們今天所帶的方法是 2006 年由 Musin 從 Delsarte's Method 派生出來的方法 (An extension of Delsarte's method) 去解決三維親吻數的問題。而過程中他不只使用了球面幾何方面的特性外，也巧妙地運用了線性規劃 (linear programming) 工具去輔助這項研究工作。 ## Lemma & Theorem <center> <img src="https://hackmd.mcl.math.ncu.edu.tw/uploads/upload_ff7146637c495f9a2b09a7335b54141e.png" style="width: 50%;"> **Figure.** Work flow </center> First, we employ Legendre polynomials $P_k(t)$ by the recurrence formula : $$ \begin{aligned} P_0 =& 1,\quad P_1 = t,\quad P_2 = \frac{3}{2}t^2 - \frac{1}{2}, \dots, \\ P_k =& \frac{t(2k - 1)}{k}P_{k - 1} - \frac{k-1}{k}P_{k-2}, \end{aligned} \tag{1} $$ or equivalently $$ P_k(t) = \frac{1}{2^kk!}\frac{d^k}{dt^k}(t^2 - 1)^k. $$ ### Lemma 1. $X = \{ x_1, x_2, \dots, x_n\}$, any finite subset of the unit sphere $S^2$ in $\textbf{R}^3$. By $\phi_{i, j} = \mathrm{dist}(x_i, x_j)$ (spherical (angular) distance between $x_i$ and $x_j$). Then $$ \sum^{n}_{i = 1}\sum^{n}_{j = 1} P_k(\cos(\phi_{i, j})) \ge 0. $$ > This Lemma will be used in Lemma 2. :::spoiler Proof of Lemma 1 First we use the addition theorem for Legendre polynomials : > [Legendre Addition theorem](https://mathworld.wolfram.com/SphericalHarmonicAdditionTheorem.html) $$ \begin{aligned} & P_k(\cos\theta_1\cos\theta_2 + \sin\theta_1\sin\theta_2\cos\varphi)\\ &= P_k(\cos\theta_1)P_k(\cos\theta_2) + 2 \sum^k_{m=1}\frac{(k-m)!}{(k+m)!}P^m_k(\cos\theta_1)P^m_k(\cos\theta_2)\cos m\varphi \\ &= P^0_k(\cos\theta_1)P^0_k(\cos\theta_2)\cos 0\varphi + 2 \sum^k_{m=1}\frac{(k-m)!}{(k+m)!}P^m_k(\cos\theta_1)P^m_k(\cos\theta_2)\cos m\varphi\\ &= \sum^k_{m=0}c_{m,k}P^m_k(\cos\theta_1)P^m_k(\cos\theta_2)\cos m\varphi, \end{aligned} $$ where $$ P^m_k(t) = (1-t^2)^{\frac{m}{2}}\frac{d^m}{dt^m}P_k(t) $$ and $c_{m,k}$ is positive number where $$ c_{m,k} = \left\{ \begin{aligned} & \frac{1}{2k} \quad \text{for } m=0\\ & 2 \frac{(k-m)!}{(k+m)!} \quad \text{otherwise}. \end{aligned} \right. $$ Then let $X = \{x_1, \dots , x_n\} \subset S^2$, and each $x_i$ have spherical coordinates $(\theta_i, \varphi_i)$. By law of cosines we have $$ \cos\phi_{i,j} = \cos\theta_i\cos\theta_j + \sin\theta_i\sin\theta_j\cos\varphi_{i,j}, \quad \varphi_{i,j} := \varphi_i - \varphi_j, $$ this implies that $$ \begin{aligned} \sum_{i,j}P_k(\cos\phi_{i,j}) &= \sum_{i,j}\sum^{k}_{m=0}c_{m,k}P^m_k(\cos\theta_i)P^m_k(\cos\theta_j)\cos m\varphi_{i,j}\\ &= \sum_m c_{m,k}\sum_{i,j}u_{m,i}u_{m,j} \cos m\varphi_{i,j}, \quad u_{m,i} = P^m_k(\cos\theta_i). \end{aligned} $$ So we need to prove that for any $u_1, \dots, u_n$ $$ \sum_{i,j} u_iu_j\cos m\varphi_{i,j} \geq 0. $$ Let $v_1, \dots, v_n \in R^2$ with coordinates $v_i = (\cos m\varphi_i, \sin m\varphi_i)$ , means that its polar coordinate is $(1, m\varphi_i)$ and $$ v = \sum_{i=1}^{n}u_iv_i, $$ then we have $$ 0 \leq ||v||^2 = \langle v, v \rangle = \sum_{i,j} u_iu_j \cos m\varphi_{i,j}. $$ Since $v_1, \dots, v_n$ are unit vector and for each $v_i, v_j$ we have $$ \begin{aligned} u_iv_i \cdot u_jv_j &= (u_i u_j) (v_i \cdot v_j)\\ &= (u_i u_j)(||v_i|| \cdot ||v_j|| \cos m\varphi_{i,j}) \\ &= u_iu_j \cos m\varphi_{i,j}. \end{aligned} $$ ::: :::spoiler Another proof of Lemma 1 Since Legendre polynomials is Gegenbauer polynomials $$ G^{(N)}_{k}(t) = \frac{t(2k + N - 4) G^{(N)}_{k-1} - (k-1)G^{(N)}_{k-2}}{k+N-3} $$ in $N = 3$ case ($G^3_k(t) = P_k(t)$). Since for any $X \subset S^{N-1}$, the matrix $(G^{(N)}_{k}(\cos\phi_{i, j}))_{ij} \in \mathbb{R}^{|X| \times |X|}$ is positive semidefinite, let $A := (P_k(\cos\phi_{i, j}))_{ij} \in \mathbb{R}^{n \times n}$ and take $x = (1, 1,\dots, 1) \in \mathbb{R}^n$, then we have $$ \sum^{n}_{i = 1}\sum^{n}_{j = 1} P_k(\cos(\phi_{i, j})) = xAx^T \ge 0. $$ ::: --- Let $$ f(t) = \frac{2431}{80}t^9 - \frac{1287}{20}t^7 + \frac{18333}{400}t^5 + \frac{343}{40}t^4 - \frac{83}{10}t^3 - \frac{213}{100}t^2 + \frac{t}{10} - \frac{1}{200} $$ > The function $f$ is a combindation of $\{P_k\}^9_{k=1}$, i.e. > $$ > f = P_{0} + \sum_{k=1}^9 c_k P_k, > $$ > > and $c_k\geq 0$ for each $k$. ### Lemma 2. $X = \{ x_1, x_2, \dots, x_n \} \subset S^2$. Then $$ S(X) = \sum^{n}_{i = 1}\sum^{n}_{j = 1} f(\cos(\phi_{i, j})) \ge n^2 $$ #### Proof of Lemma 2 : The expansion of $f$ in terms of $P_k$ is $$ f = \sum^9_{k=0}c_kP_k = P_0 + \frac{8}{5}P_1 + \frac{87}{25}P_2 + \frac{33}{20}P_3 + \frac{49}{25}P_4 + \frac{1}{10}P_5 + \frac{8}{25}P_9 $$ where $c_k \geq 0$ for $k = 1, \dots, 9$. By Lemma 1 we have $$ S(X) = \sum^9_{k=0}c_k\sum^n_{i=1}\sum^n_{j=1}P_k(\cos(\phi_{i,j})) \geq \sum^n_{i=1}\sum^n_{j=1}c_0P_0 = n^2. $$ --- ### Lemma 3. Let $X = \{ x_1, x_2, \dots, x_n \} \subset S^2$ where $\phi_{i, j} \geqslant 60^{\circ}$ $\forall i\neq j$. Then $$ S(X) = \sum^{n}_{i = 1}\sum^{n}_{j = 1} f(\cos(\phi_{i, j})) < 13n $$ Proof of Lemma 3 will be showed in next section. ### Theorem: $k(3) = 12$ #### Proof of theorem : By Lemma 2 and Lemma 3, we have that $13 \cdot n > S(X) \geq n \cdot n$. So we have $n \leq 12$, and by $k(3) \geq 12$, then we conclude that $k(3) = 12$. ## Proof of Lemma 3 We need one fact form spherical trigonometry, namely law of cosine : $$ \cos\phi = \cos\theta_1\cos\theta_2 + \sin\theta_1\sin\theta_2\cos\varphi $$ > 球面餘弦定理之證明 : > > 如下圖三角形所示，並令 $O$ 為單位圓心，由於在單位球面上三角形的形狀並不會因移動與旋轉改變，所以我們可以對三角形做以下操作 : > > 1. 將三角形移動到 $A$ 點在北極點上 (即 $(0, 0, 1)$)，並將其旋轉至 $B$ 點在本初子午線上 > 2. 此時 $B$ 點與 $C$ 之球座標分別為 $(1, \theta_1, 0)$ 與 $(1, \theta_2, \varphi)$ > 3. 將 $B$ 點與 $C$ 點之座標轉為直角坐標，則此時 $B = (\sin \theta_1, 0, \cos \theta_1)$ 與 $C = (\sin \theta_2 \cos \varphi, \sin \theta_2 \sin \varphi, \cos \theta_2)$ > 4. 由於 $\cos \varphi$ 為 $\overline{OB}$ 與 $\overline{OC}$ 向量之內積，將其內積後則完成球面餘旋定理之證明。 <center><img width='150px' src='https://hackmd.mcl.math.ncu.edu.tw/uploads/upload_a5e2ebd9a48524188f26f9310f4d4afc.png'></center> Now we prove lemma 3 by following steps. ### Step 1. Use properties of $f$ to simplify the proof $f(t)$ have following properties: 1. $f(t)$ is monotone decreasing on the intervel $[-1, -t_0]$; 2. $f(t) < 0$ for $t \in(-t_0, \frac{1}{2}]$; 3. $f(-t_0) = 0, t_0 \approx 0.5907$.  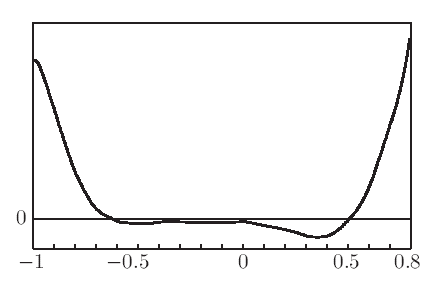#### Simplify the proof Let $$ S_i(X) := \sum^{n}_{j = 1} f(\cos(\phi_{i, j})), \quad S(X) = \sum^{n}_{i = 1} S_i(X). $$ So if we prove $$ S_i(X) < 13 \text{ for } i = 1, 2, \dots, n, $$ then $$ S(X) < 13n. $$ Since $f(t) \ge 0$ for $t \in [-1, -t_0]$, define $$ J(i) := \{ j: \cos(\phi_{i, j}) \in [-1, -t_0] \}, $$ means the collection of points $x_j$ where $f(\cos\phi_{i, j}) \ge 0$ for fixed $x_i$, then we obtain $$ S_i(X) = \sum^{n}_{j = 1} f(\cos(\phi_{i, j})) \le T_i(X) := f(1) + \sum_{j \in J(i)}f(\cos(\phi_{i, j})). $$ Define $\theta_0 = \arccos(t_0) \approx 53.794^{\circ}$ and $e_0 = −x_i$ is the antipodal point to $x_i$, then all $x_{j}$, $j \in J(i)$, lie inside the spherical cap of center $e_0$ and radius $θ_0$. <center> <img width='200px' src='https://hackmd.mcl.math.ncu.edu.tw/uploads/upload_df3003756143a24b5d317f48c8147f47.png'> </center> Let's consider points $e_0, y_1, \dots, y_m$ such that $$ \begin{aligned} \phi_{i, j} =& \mathrm{dist}(y_i, y_j) \ge 60^{\circ}, \forall i \neq j \\ \theta_i :=& \mathrm{dist}(e_0, y_i) < \theta_0 \text{ for } 1 \leq i \leq m. \end{aligned} \tag{2} $$ Let $$ \mu = \text{the highest value of } m \text{ s.t. } (2) \text{ holds.} $$ Suppose that $0 \le m \le \mu$ and $Y = \{y_1, \dots, y_m \}$ satisfies $(2)$. Define $$ H(Y) = H(y_1, \dots, y_m) := f(1) + f(−\cos \theta_1) + \dots + f(−\cos \theta_m) $$ and maximum of $H(Y)$ $$ \begin{aligned} h_m :=& \sup_{Y}\{ H(Y) \}; \\ h_{\max} :=& \max \{ h_0, h_1, \dots , h_\mu \}. \end{aligned} $$ Then $$ T_i(X) \le h_m \text{ where } m = |J(i)|, $$ so we only need to prove $h_{\max} < 13$. ### Step 2. Compute $\mu$ For fixed $x_i$ as south pole, we have $Y = \{ y_1, \dots, y_m \} \subset S^2$, where $e_0$ is north pole and $y_i$ has polar coordinates $(\theta_i, \varphi_i)$. <!-- x 的極座標要特別講一下 --> > Note that this coordinates different from basic polar coordinates. $\theta_i$ is $dist(e_0, y_i)$ and $\varphi_i$ is angle between $y_i$ and prime meridian. > Recall law of consine : $\cos(\phi_{i, j}) = \cos\theta_i\cos\theta_j + \sin\theta_i\sin\theta_j\cos(\varphi_i - \varphi_j)$. Note that $\theta_i > 0$ for $m \ge 2$. By $\cos\phi_{i, j} \le \frac{1}{2}$, we have $$ \tag{3} \cos(\varphi_i - \varphi_j) \le \frac{\frac{1}{2} - \cos\theta_i\cos\theta_j}{\sin\theta_i\sin\theta_j}. $$ Let $$ Q(\alpha, \beta) := \frac{\frac{1}{2} - \cos\alpha\cos\beta}{\sin\alpha\sin\beta}, $$ then $$ Q'_\alpha(\alpha, \beta) = \frac{\partial Q(\alpha, \beta)}{\partial \alpha} = \frac{2 \cos\beta - \cos\alpha}{2\sin^2\alpha\sin\beta}. $$ > By symmetric of $Q$, we only need to check the partial derivative of $\alpha$ If $0 < \alpha, \beta \le \theta_0$, then $$ \cos\beta > \frac{1}{2} (\text{since }\theta_0 < 60^{\circ})\Rightarrow Q'_\alpha(\alpha, \beta) > 0 $$ $$ \Rightarrow Q(\alpha, \beta) \le Q(\theta_0, \beta) = Q(\beta, \theta_0) \le Q(\theta_0, \theta_0). $$ Therefore $$ \cos(\varphi_i - \varphi_j) \le \frac{\frac{1}{2} - \cos^2\theta_0}{\sin^2\theta_0} = \frac{{1}{2} - t_0^2}{1 - t_0^2}. $$ Since $$ \arccos(\frac{\frac{1}{2} - t_0^2}{1 - t_0^2}) \approx 76^{\circ} > 72^{\circ}. $$ We conclude that $m \le 4.$ ### Step 3. Prove $h_0, h_1 < 13$ #### $h_0$ : $$ h_0 = f(1) = 10.11 < 13. $$ #### $h_1$ : Since $f(-\cos\theta)$ is monotone decrease in $\theta$ on $[0, \theta_0]$, for $m = 1$, $H(y_1) = f(1) + f(-\cos\theta_1)$ has maximum at $\theta_1 = 0$, > If $y_1$ closer to $e_0$, $f(-\cos \theta_1)$ will be larger. $$ h_1 = f(1) + f(-1) = 12.88 < 13. $$ ### Step 4. Optimal deployments of $y_i$ for $m = 2, 3, 4$ Now we consider a best arrangement $Y$ that makes $H(Y) = h_m$ for $m = 2, 3, 4$. Note that our objective is to make vertices close to $e_0$. Overall, * $m=2$ yields $e_0\in y_1 y_2$ and $\mathrm{dist}(y_1, y_2) = 60^{\circ}$. * $m=3$ yields $\Delta_3 = y_1 y_2 y_3$ being a spherical regular triangle with edge length $60^{\circ}$. * $m=4$ yields $\Delta_4 := \mathrm{conv\ } Y$ (the spherical convex hull of $Y$); moreover, $\Delta_4$ being a spherical rhomb (菱形) with edge length $60^{\circ}$. > 留意到三維原文提供了簡化的證明。實際上，比較嚴格的證明版本是在他自己撰寫的另一篇論文當中，收錄在《數學年鑑》中探討四維親吻數問題。 > > 因此如果要找比較嚴謹的證明，可以找 > * 四維原文：Musin, O. (2008). [*The Kissing Number in Four Dimensions*](https://arxiv.org/pdf/math/0309430.pdf). Annals of Mathematics, 168(1), second series, 1-32. > * 或是筆者自己整理的速筆：[Strict Inference of Optimal form of Spherical Code for Three Dimensions](https://codimd.mcl.math.ncu.edu.tw/s/9hzDsFLmp) > > 整體架構因為有其他符號需要補充，放到本文會稍嫌複雜。所以僅提供整個框架： > > 1. 首先他先說明何種 $Y$ 是不可約的 (irreducible)：簡單來講就是不能讓任一點 $y_i$ 能夠再更靠近 $e_0$. > 2. 接著說明任意點數組合成的形狀 $\Delta_m$ 必定是凸多邊形， > 3. 並且註記到任何 $Y$ 使得 $H(Y) = h_m$，本身 $Y$ 一定是不可約的， > 4. 再者說明 $e_0\in\Delta_m$，且對於任何 $i$，必定存在至少一個 $j\neq i$ 使得 $\phi_{i,j} = 60^{\circ}$. > 5. 結合上述資訊，可以證明在 $m=3,4$ 時，對於任何 $i$，必定存在兩個以上 $j\neq i$ 使得 $\phi_{i,j} = 60^{\circ}$，而這個資訊又足夠證明 $\Delta_3$ 會是邊長 $60^{\circ}$ 的正三角形，且 $\Delta_4$ 會是邊長 $60^{\circ}$ 的菱形。 > > [name=Yu-Kai Lin] For completion we left the simplified proof in [Appendix 1](#Appendix-1). Based on above knowledge, now we prove $h_\max < 13$. ### Step 5.1. $h_2 < 13$ Define $$ F_1(\psi) := \max_{\frac{\psi}{2} \le \theta \le \theta_0} \{ \tilde{F}_1(\theta, \psi) \}, $$ where $$ \tilde{F}_1(\theta, \psi) = f(-\cos\theta) + f(-\cos(\psi - \theta)). $$ > Note that: > > * This consider the case $e_0\in y_i y_j$. > * $\theta$ is the distance of $y_i$ and $e_0$. > * $\psi$ is the distance of $y_i$ and $y_j$. > * With $\theta$ and $\psi$, $\mathrm{dist}(y_j, e_0)$ can be uniquely determined. > * As mentioned, $F_1$ is monotone decreasing in $\psi$. |  | 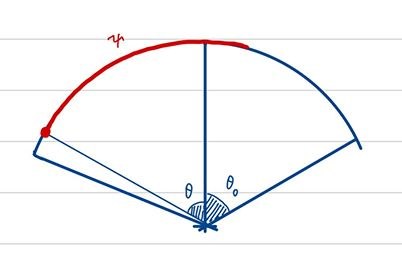 | 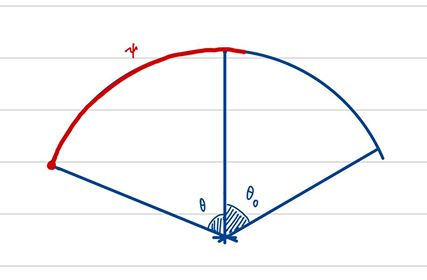 | | ------------------------------------------------------------------------------------------- | ------------------------------------------------------------------------------------------- | -------- | | $\theta=\psi/2$ | $\theta_0 < \theta < \psi/2$ | $\theta=\theta_0$ | Then if $\mathrm{dist}(y_i, y_j) = \psi$, we have $$ \tag{4} f(-\cos\theta_i) + f(-\cos\theta_j) \le F_1(\psi). $$ Therefore, $$ H(y_1, y_2) \le h_2 = f(1) + F_1(60^{\circ}) \approx 12.8749 < 13. $$ ### Step 5.2. $h_4 < 13$ <center> <img src="https://hackmd.mcl.math.ncu.edu.tw/uploads/upload_bc21da400600adc236b9232e7621e8a7.png" width=400> </center> Define $d_1 = \mathrm{dist}(y_1, y_3)$ and $d_2 = \mathrm{dist}(y_2, y_4)$. With orthogonality, $$ \frac{1}{2} = \cos(\mathrm{dist}(y_1, y_2)) = \cos\frac{d_1}{2}\cos\frac{d_2}{2} + \sin\frac{d_1}{2}\sin\frac{d_2}{2}\cos90^{\circ} = \cos(\frac{d_1}{2})\cos(\frac{d_2}{2}). $$ Now define another function $\rho$ given as $$ \rho(s) := 2 \arccos(\frac{1}{2\cos(\frac{s}{2})}). $$ Note that this function has following properties: 1. $\rho$ is monotone decreasing in $(0, \pi)$, 2. $\rho(d_1) = d_2$, 3. $\rho(d_2) = d_1$, 4. $\rho(90^{\circ}) = 90^{\circ}$, and 5. $\rho(\rho(s)) = s$. Assume $d_1 \le d_2$. The inequalities $\theta_i \le \theta_0$ yield $d_2 \le 2\theta_0$, then we have $$ \rho(2\theta_0) \le \rho(d_2) = d_1 \le 90^{\circ} \le d_2 \le 2\theta_0. $$ Now consider two cases: 1. $\rho(2\theta_0) \le d_1 < 77^{\circ}$, 2. $77^{\circ} \le d_1 \le 90^{\circ}$. #### Case 1: $\rho(2\theta_0) \le d_1 < 77^{\circ}$ With inequalities $$ f(-\cos\theta_1) + f(-\cos\theta_3) \le F_1(d_1) \le F_1(\rho(2\theta_0)), $$ and $$ f(-\cos\theta_2) + f(-\cos\theta_4) \le F_1(d_2) = F_1(\rho(d_1)) \le F_1(\rho(77^{\circ})), $$ obtains $$ H(Y) < f(1) + F_1(\rho(77^{\circ})) + F_1(\rho(2\theta_0)) \approx 12.9171 < 13. $$ #### Case 2: $77^{\circ} \le d_1 \le 90^{\circ}$ With similar procedure, we have $$ H(Y) \le f(1) + F_1(77^{\circ}) + F_1(90^{\circ}) \approx 12.9182 < 13. $$ Therefore, $h_4 < \max\{12.9172, 12.9183\} < 13.$ ### Step 5.3. $h_3 < 13$ <small>Final step !!</small> <center> <img src='https://hackmd.mcl.math.ncu.edu.tw/uploads/upload_b4a91d6f9e95849ddbdda8313f297de4.png' width=300> </center> For $m = 3$, we have $$ H(Y) = f(1) + f(-\cos\theta_1) + f(-\cos\theta_2) + f(-\cos\theta_3). $$ Without loss of generality, we assume $$ \theta_1 \le \theta_2 \le \theta_3 \le \theta_0. $$ In this case $R_0 \le \theta_3 \le \theta_0$, where $R_0 = \arccos\sqrt{2/3} \approx 35.2644^{\circ}$ is the (spherical) circumradius of $\Delta_3$. Let $y_c$ be the center of $\Delta_3$. We have $\gamma := \angle y_1y_3y_c = \angle y_2y_3y_c$. With the low of cosines for the triangle $y_1 y_3 y_c$, we get $\gamma = \arccos\sqrt{2/3}$, i.e. $\gamma = R_0$. Denote $\angle e_0y_3y_c$ by $u$, then $$ \cos\theta_1 = \cos60^{\circ}\cos\theta_3 + \sin60^{\circ}\sin\theta_3\cos(R_0 - u),\\ \cos\theta_2 = \cos60^{\circ}\cos\theta_3 + \sin60^{\circ}\sin\theta_3\cos(R_0 + u). $$ where $0 \le u \le u_0 := \arccos\left(\cot\theta_3/\sqrt{3}\right) - R_0$. Observe that * If $u = u_0$, then $\theta_2 = \theta_3$, * If $u = 0$, then $\theta_1 = \theta_2$, * If $0 < u < u_0$, then $\theta_1 < \theta_2 < \theta_3$ Now define another function $$ F_2(\psi) := \max_{0\leq u \leq u_0} \tilde F_2 (u, \psi), $$ where $$ \begin{aligned} \tilde F_2 (u, \psi) &= f(-\cos \theta_1) + f(-\cos \theta_2) \\ &= f(- \cos60^{\circ}\cos\psi - \sin60^{\circ}\sin\psi\cos(R_0 - u)) \\ &\qquad + f(-\cos60^{\circ}\cos\psi - \sin60^{\circ}\sin\psi\cos(R_0 + u)). \end{aligned} $$ > Also note that: > > * $\psi$ is the distance of $y_3$ and $e_0$. > * With $u$ and $\psi$, $\theta_1$ and $\theta_2$ can be uniquely determined. > * With fixed $\psi$, $\tilde F_2 (u, \psi)$ is a polynomial of degree 9 in $s = \cos u$. > * $F_2(\psi)$ is monotone increasing function in $\psi$ on $[R_0, \theta_0]$ |  | 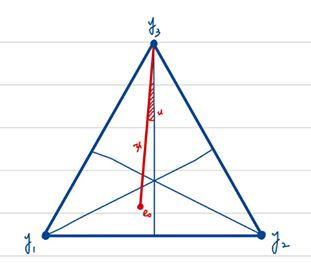 | 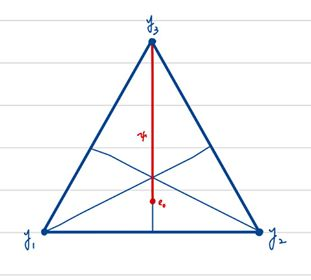 | | ------------------------------------------------------------------------------------------- | ------------------------------------------------------------------------------------------- | ------------------------------------------------------------------------------------------- | | $u=u_0$ | $0<u<u_0$ | $u=0$ | Consider a finite partition of interval $[R_0, \theta_0]$: $$ \{ \psi_1, \dots, \psi_6 \} = \{ R_0, 38^{\circ}, 41^{\circ}, 44^{\circ}, 48^{\circ}, \theta_0 \}. $$ Recall that * $F_2(\psi)$ is monotone increasing on $[R_0, \theta_0]$, and * $f(-\cos\psi)$ is monotone decreasing on $[R_0, \theta_0]$, therefore, for $\theta_3 \in [\psi_i, \psi_{i+1}]$, $$ H(Y) = H(y_1, y_2) + f(-\cos\theta_3) < w_i := F_2(\psi_{i+1}) + f(-\cos\psi_i). $$ With $$ \{ w_1, \dots, w_5 \} \approx \{ 12.9425, 12.9648, 12.9508, 12.9606, 12.9519 \}, $$ we have $$ h_3 < \max\{ w_i \} < 13. $$ Thus, $h_m = \max\{h_0, h_1, h_2, h_3, h_4, h_5\} < 13$. ### Appendix 1 #### Case $m=2$ * If $e_0\not\in y_1 y_2$, then the whole arc $y_1 y_2$ can be shifted towards $e_0$. * If $\mathrm{dist}(y_1, y_2) > 60^{\circ}$, then $y_1$ (and $y_2$) can be shifted towards $e_0$. #### Case $m=3$ * As above, $e_0 \in \Delta_3$, otherwise the whole triangle can be shifted towards $e_0$. * Suppose $\mathrm{dist}(y_1, y_i) > 60^{\circ}$ for $i=2, 3$, then $\mathrm{dist}(y_1, e_0)$ can be decreased. This follows that for any $y_i$, exists $j$ such that $\mathrm{dist}(y_i, y_j) = 60^{\circ}$. Therefore, at least two sides of $\Delta_3$ (assume $y_1 y_2$ and $y_1 y_3$) have length $60^{\circ}$. * Also $\mathrm{dist}(y_2 y_3) = 60^{\circ}$, conversely $y_3$ can be rotated about $y_1$ by a small angle towards $e_0$:  #### Case $m=4$ * Assume $y_4\in y_1 y_2 y_3$. The great circle through y4 that is orthogonal to the arc $e_0 y_4$ divides $S_2$ into two hemispheres: $H_1$ and $H_2$. Suppose $e_0 \in H_1$, then at least one $y_i$ (say $y_3$) belongs to $H_2$.  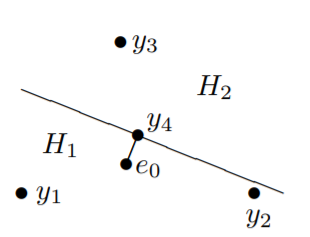* Note that the angle $\angle e_0 y_4 y_3 > 90^{\circ}$, which yields $\mathrm{dist}(e_0, y_3) > 60^{\circ} > \theta_0$ -- a contradiction. * So $\Delta_4 := \mathrm{conv\ } Y$. * Note that the diagonals of $\Delta_4$ cannot be both of lengths $60^{\circ}$. Conversely, at least one side of $\Delta_4$ is of length less than $60^{\circ}$ . Thus, $\Delta_4$ is a spherical equilateral quadrangle (rhomb) with edge length $60^{\circ}$. ### Appendix 2 * [Verification of Kissing number problem](https://hackmd.mcl.math.ncu.edu.tw/ZvoSHkFvTf20S4VXX5I0sg)